6ta Actividad - Repaso Generalizado
Hola chicos.... en el posteo anterior, utilizabamos lo aprendido de entornos, para poder encontrar el DOMINIO y el RANGO DE LAS FUNCIONES....
Y anteriormente aprendimos a encontrar las raices de una cuadratica (donde la grafica corta, o no, al eje x)
En esta oportunidad vamos a ver, en base a diferentes ejemplos, varios conceptos..... que son fáciles de ver a través de las graficas propuestas...
Ellos son: CONTINUIDAD, CRECIMIENTO Y DECRECIMIENTO, MAXIMOS Y MINIMOS, EJE DE SIMETRIA(analizado en algunas cuadráticas) y PARIDAD
Metodologia de trabajo:
En total vamos a trabajar con 7 funciones..... 3 lineales y 4 cuadráticas
En el caso de las 2 lineales primeras, analizaremos CONTINUIDAD, CRECIMIENTO Y DECRECIMIENTO... en el CASO 7 veremos PARIDAD
CASO 1
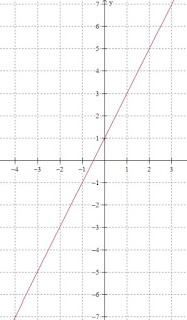
f(x) = 2x+1
tabla de valores grafica
OBSERVEMOS:
* La columna de las X arranca en -4, y va creciendo de a 1 hasta llegar 3, es decir CRECE
* La columna de las Y arranca en -7, y va creciendo de a 2 hasta llegar a 7, tambien CRECE
Cuando la columna de las X CRECE y, al mismo tiempo la columna de las Y tambien CRECE.... LA FUNCION ES CRECIENTE
OBSERVEMOS OTRA VEZ..... esta definición que viene es poco ortodoxa.... ya van a tener tiempo (en sus próximas carreras universitarias) de aprenderla de manera mas "académica".... Una función es CONTINUA, cuando "no levanto el lápiz del papel" para graficarla.....
Les cuento que todas las funciones lineales y cuadráticas son CONTINUAS
CASO 2
F(x) = -2x + 1
tabla de valores grafica


OBSERVEMOS:
* La columna de las X arranca en -2, y va creciendo de a 1 hasta llegar 3, es decir CRECE
* La columna de las Y arranca en 5, y va DECRECIENDO( lo contrario de creciendo) de a 2 hasta llegar a -3,
Cuando la columna de las X CRECE y, al mismo tiempo la columna de las Y DECRECE.... LA FUNCION ES DECRECIENTE
Obviamente, y como lo decimamos en el CASO 1, esta también en CONTINUA
AHORA SE VIENEN LAS CUADRATICAS......
CASO 3
F(x) = 2x2
tabla de valores grafica


OBSERVEMOS:
Aquí están pasando algunas cositas que son propias de las cuadráticas
* La gráfica es una curva, primera diferencia con las lineales, y en un punto ESPECIAL.... si viene DECRECIENDO, deja de hacerlo y se transforma en CRECIENTE(esto pasa cuando el termino "a" que acompañe a la x2 es positivo......
Y.....
si viene CRECIENDO, deja de hacerlo y se transforma en DECRECIENTE(esto pasa cuando el termino "a" que acompañe a la x2 es NEGATIVO...... lo vamos a ver en el CASO 4
Ese punto en cuestión se denomina MINIMO, si es cóncava hacia arriba...... y MAXIMO, si es cóncava hacia abajo
Aquí vamos a utilizar otra vez lo que aprendimos de entornos del postea anterior que nos enseño la profe Natalia
En este caso la función es DECRECIENTE en el intervalo (-00 , 0]
Y es creciente en el intervalo [0 , +00)
Siendo el punto (0 , 0) el MINIMO de esta función
* Miren el eje Y.... en esta grafica es una especie de espejo...... ya que si echamos un vistazo a la tabla de valores, para los valores de x=-2 y x=2, el resultado es 8....... para x=-1 y para x=1 el valor de y es 2 y lo mismo pasaría en 3 y -3.... 4 y -4.... etc
Cuando ocurre esto, se dice que la función es PAR
*Al mismo tiempo, ese eje Y, es eje de simetría de la función, (lo vamos a aclarar un poco mas a partir del CASO 5)
CASO 4
F(x) = -2x2
tabla de valores grafica

Vamos a aprovechar lo que aprendimos en el CASO 3.
* Esta es una cuadrática cuyo término "a" es negativo.... entonces, ya sabemos que es cóncava hacia abajo, por lo tanto esta tendrá un MAXIMO... y esta ubicado en el punto (0 , 0)
* A diferencia de la anterior esta funcion es CRECIENTE en el intervalo (-00 , 0] y DECRECIENTE
en el intervalo [0 , +00)
*Mantiene al eje Y como EJE DE SIMETRIA (insisto, lo explicaremos mejor en el caso 5)
*y como la anterior es una funcion PAR, ya que tanto para x = 2 y para x = -2 el resultado es -8
Ahora que ya avanzamos un poco mas.... damos mas rigor a la definición de cuando una función es PAR....
Una función es Par si se cumple la siguiente condición:
Para todo x -------- F(x) = F(-x) -----------> Ejemplo F(2) = F(-2) = -8
CASO 5 (otra cuadrática, la penúltima)
F(x) = x2+2x+2
tabla de valores grafica
Si hacemos el estudio completo completo..... como se les va a pedir en los ejercicios, dir+iamos lo siguiente:
DOMINIO ---> R
IMAGEN ----> [ 1 , +00)
CONTINUIDAD es continua
CRECIMIENTO Y DECRECIMIENTO (aquí deberíamos encontrar el máximo o mínimo para empezar)
PARIDAD Y/O EJE DE SIMETRIA
Busquemos el mínimo de la función (como es cóncava hacia arriba porque "a" es positivo) esta cuadrática tiene un mínimo, y calculamos EL VERTICE, que será también el mínimo para este caso
Luego de hacer los calculitos...... el vértice de esta funcion es V(-1 , 1)
Y nos sirve para introducir el último de los conceptos, que es el de EJE DE SIMETRIA....., En este caso, va a ser una recta paralela al eje y, que, OBLIGATORIAMENTE, pasara por el punto x del vértice (en este caso, pasará por -1)
y asi cumplimos con todos los ítems de teoria..... que vamos a reafirmar en el CASO 6, y nos faltaría saber cuando una función es impar, que analizaremos en el CASO 7
CASO 6
F(x) = -2x2+4x+2
tabla de valores Gráfica
Ahora tomamos envion..... y decimos:
DOMINIO ---> R
IMAGEN ----> (-00 , 4 ]
CONTINUIDAD es continua
VERTICE (1 , 4)
CRECIENTE (-00 , 1]
DECRECIENTE [1 , +00]
EJE DE SIMETRIA x = 1
Que tal.... si los conceptos que fuimos dando se entendieron..... así de rápido sale todo esto......
BONUS TRACK - CASO 7
F(x) = 2x
tabla de valores Gráfica
Esta es una lineal que no tiene término ORDENADA AL ORIGEN...... y aunque tengan pendiente negativa, pero sin ORDENADA AL ORIGEN... estas funciones son IMPARES
FUNDAMENTAMOS LA PARIDAD DE LAS FUNCIONES:
Una función es par si F(x) = F(-x) (CASO 3 Y CASO 4)
Una función es impar si F(x) = -F(-x)
Ejemplo F(2) = 4
y - F(-2) = - (-4) o sea 4
y convenimos......
TODAS LAS FUNCIONES LINEALES QUE NO TENGAN ORDENADA AL ORIGEN.... SON IMPARES
Ahora los Ejercicios:
DETERMINAR: Dominio, Imagen (ojo las cuadraticas) , continuidad, crecimiento y decrecimiento(en el caso que hubiera ambos marcar los intervalos), máximos o mínimos (si los hubiera), Raíces(si las hubiera), Eje de simetría y/o paridad..... recuerden revisar la teoría, no todas cumplen con todas estas condiciones
a) F(x) = -3x2 +
6x - 1
b) G(x) = 4x+1
c) H(x) = x2 + 3x + 2
d) I(x) = -3x
e) J(x) = -4x
f) K(x) = -3x2
Exitos.... cualquier cosita me consultan.....
Fecha de entrega 15 de octubre